Plane Strain Fracture

When we started discussing how to characterize a cracked structure we introduced the concept of a singularity dominated region and extracted a single parameter from it \(K\) which we claimed can fully characterize the crack tip fields.

The value of \(K\) at which a test specimen fails is denoted \(K_{c}\) and is a material parameter (i.e. independent on geometry).

  • How can be concile the \(K\) approach to fracture arising from LEFM with the presence of plasticity at the crack tip we discussed last week?

  • What are the conditions for which the \(K\) approach still holds?

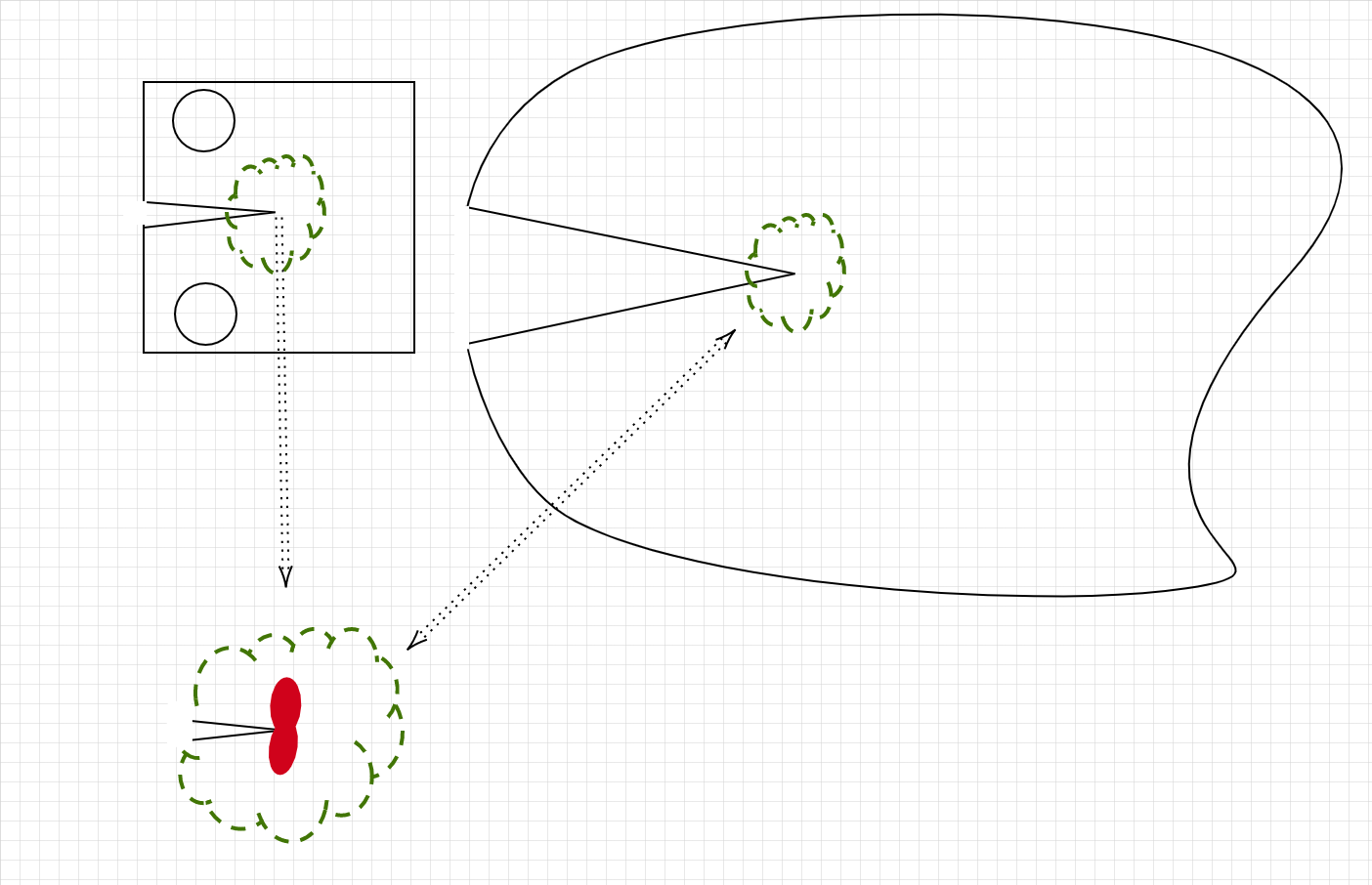
Kdominance

Inlight of the approached we saw last time for coping with the presence of a plastic zone at the crack tip, we may claim that \(K\) can still be used to characteriz the crack tip fields, even in the presence of local yielding, given that \(\color{red}{r_p}\) is sufficeintly small to keep inside the \(1/\sqrt{r}\) dominant region.

Example:

What is sufficiently small? how can we estimate if a measured \(K\) is valid?

Assume you are measuring the \(K_I\) ofan infinite plate with a through crack under remote tensile load (we solved this before).

For the crack symmetry plane (\(\theta=0\)) we can write down the stresses to be

\[\begin{split} \sigma_{yy} = \frac{\sigma (a+r)}{\sqrt{2ar+r^2}} \\ \sigma_{xx} = \frac{\sigma (a+r)}{\sqrt{2ar+r^2}} -\sigma \end{split}\]

For \(r \to 0\) we obtain

\[ \sigma_{xx}^{r\to 0}=\sigma_{yy}^{r\to 0} = \frac{K_I}{\sqrt{2 \pi r}} \]

Obviously, for some ratio of \(r/a\) the stresses estimate arising from limit of \(r \to 0\) will drift away from the full solution.

A. Plot the ratios:

\[\begin{split} 1. \ \ \frac{\sigma_{xx}}{\sigma_{xx}^{r\to 0}} \\ 2. \ \ \frac{\sigma_{yy}}{\sigma_{yy}^{r\to 0}} \end{split}\]

as a fuction of \(r/a\).

B. Use the plane strain plastic zone expression we obtained and set \(\color{red}{r_p}\) to [a/250 a/100 a/50 a/25 a/10 a/5]. Estimate the resulting \(K_I\)

C.Can you estimate the stress (in terms of \(\sigma / \color{red}{\sigma_{y}}\) at which the use of K as the characterizing parameter becomes probematic for each of the \(\color{red}{r_p}\) above?

\({\color{red}{r_p}}=a/50\)

using the above ratio we obtain

\[ a=\frac{50}{6 \pi} \left( \frac{K_I}{\color{red}{\sigma_{y}}} \right)^2 \]

After some algebra we obtain

\[ K_I = 0.35{\color{red}{\sigma_{y}}}\sqrt{\pi a} \]

So for \(\sigma \gt 0.35{\color{red}{\sigma_{y}}}\) the usage of \(K\) as the only characterizing parameter becomes problematic

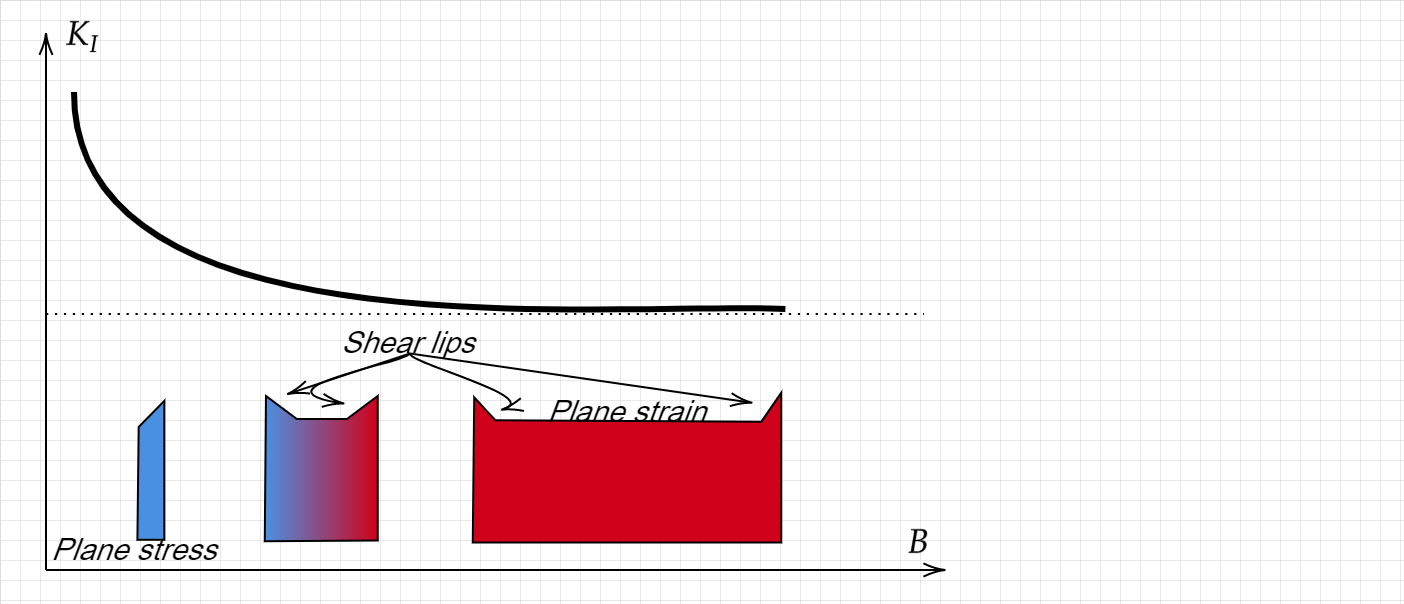
We saw that by comparing the plastic zone size \({\color{red}{r_p}}\) to a characteristic length of the system (\(a\)) we can enforce limitations of a fracture test. But that is not the only lengthscale in our tests/structures

Back in the 1960’s the fracture community noticed that the measured values of \(K\) for agiven material exhibited a thickness dependence. The coined the terms Plane strain fracture and Plane stress fracture, in part due to the fact the 3D crack analysis is highlycomplex analytically and FEM was not widely spread. Today, we know that these two terms are misleading and the thickness effect oberved experimentally can be understood by considering the 3D stress state.

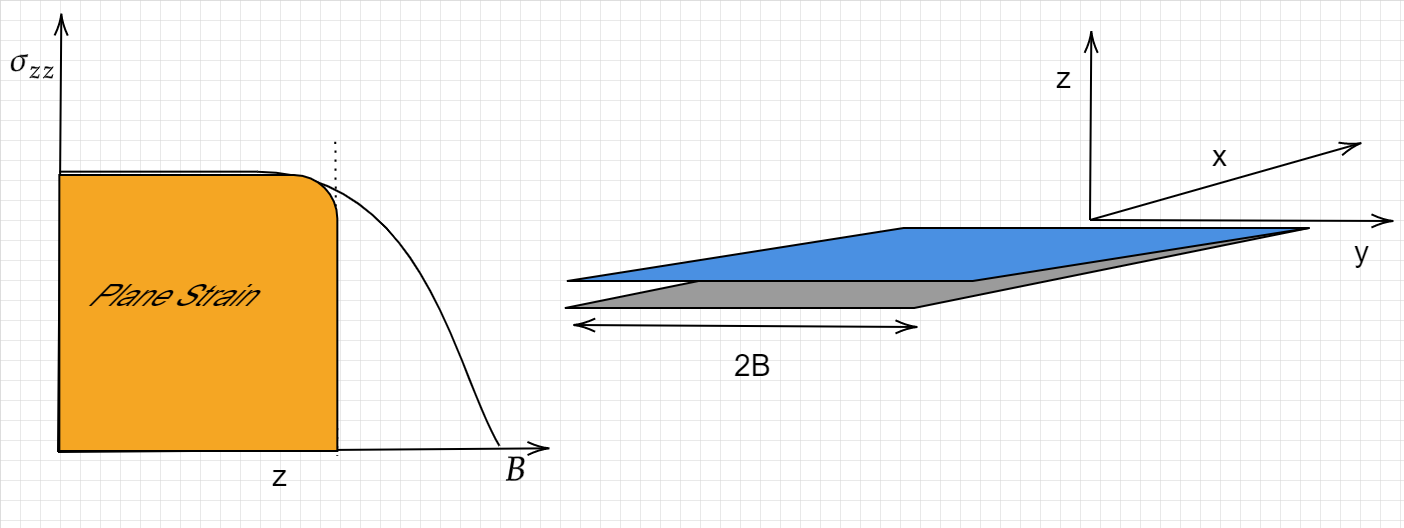
Kdominance

The plastic zone estimates we dealt with beofre are used in teh ASTM standards (e.e. ASTM E399) as a criteria for the validity of a \(K_I\) measurment.

Knowing the \({\color{red}{\sigma_y}}\) of our material, and after measuring the \(K_{Ic}\) from an experiment, we will use

\[ a,B,(W-a) \ge 2.5 \left ( \frac{K_{IC}}{{\color{red}{\sigma_y}}} \right ) \]

as a criteria for accepting our test result.

Kdominance

previous

Crack Tip Plasticity

next

Testing for Toughness