J controlled fracture

HRR

Note

The HRR fields were published in 1968 by (J.R. Rice and G.F> Rosengren)[https://doi.org/10.1016/0022-5096(68)90013-6] and by (J.W. Hutchinson)[https://doi.org/10.1016/0022-5096(68)90014-8]

The HRR field, named after Hutchinson Rice and Rosengren is the solution for the mechanical fields at the tip of a stationary crack in a power law material.

The load is assumed to increase monotonically, thus allowing the use of the deformation theory of plasticity. As we mentioned previously, the deformation theory theory can be thought of as non-linear elasticity with the relation.

\[ \frac{\epsilon}{\epsilon_y} = \alpha \left ( \frac{\sigma}{\sigma_y}\right)^n \]

Writing down the \(J\) integral for \(r \to 0\) :

\[ J=\int_{-\pi}^{\pi} W n_1 - T_i \frac{\partial u_i} { \partial x_1} rd \theta \]

We can estimate that the integrand have the form of \(\frac{f(\theta)}{r}\)

This implies that

\[ \sigma \cdot \epsilon \propto \frac{g(\theta)}{r} \]

if we expand \(\sigma_{ij}\) into a series around \(r \to 0\) such that

\[ \sigma_{ij}(r,\theta) = \sum_s r^s\sigma_{ij}^*(\theta,s) \]

we can obtain for \(r \to 0\) where the plastic strains are much greater than the elastic ones:

\[ \epsilon_{ij} =\epsilon^p_{ij} =r^{sn}\gamma^*_{ij}(\theta,s) \]

Since we required earlier that \(\sigma \cdot \epsilon \propto r^{-1}\) it implies that \(s+sn=-1\) and thus \(s\) which will lead to the strongest singularity is

\[ s=\frac{-1}{1+n} \]

Now, the HRR stress and strain fields (for \(r \to 0\)) are given by:

\[\begin{split} \sigma_{ij} = \sigma_y k_n r^{-1/(n+1)}\sigma_{ij}^*(\theta,n) \\ \epsilon_{ij} = \epsilon_y k_n^n r^{-n/(n+1)}\epsilon_{ij}^*(\theta,n) \end{split}\]

Note

For \(n \to 1\) we obtain a \(r^{-1/2}\) singularity

Using the HRR fields in the \(J\) integral will lead to

\[ J=\sigma_y \epsilon_y \alpha k_n^{n+1} \int_{-\pi}^{\pi} f_{ij}^*(\theta,n)d\theta = \sigma_y \epsilon_y \alpha k_n^{n+1} I_n \]

With \(k_n\) being:

\[ k_n=\left( \frac{J}{\alpha \sigma_y \epsilon_y I_N}\right)^{1/(n+1)} \]

and finally

\[\begin{split} \sigma_{ij} = \sigma_y \left( \frac{J}{r\alpha \sigma_y \epsilon_y I_N}\right)^{1/(n+1)}\sigma_{ij}^*(\theta,n) \\ \epsilon_{ij} = \epsilon_y\left( \frac{J}{r\alpha \sigma_y \epsilon_y I_N}\right)^{n/(n+1)}\epsilon_{ij}^*(\theta,n) \end{split}\]

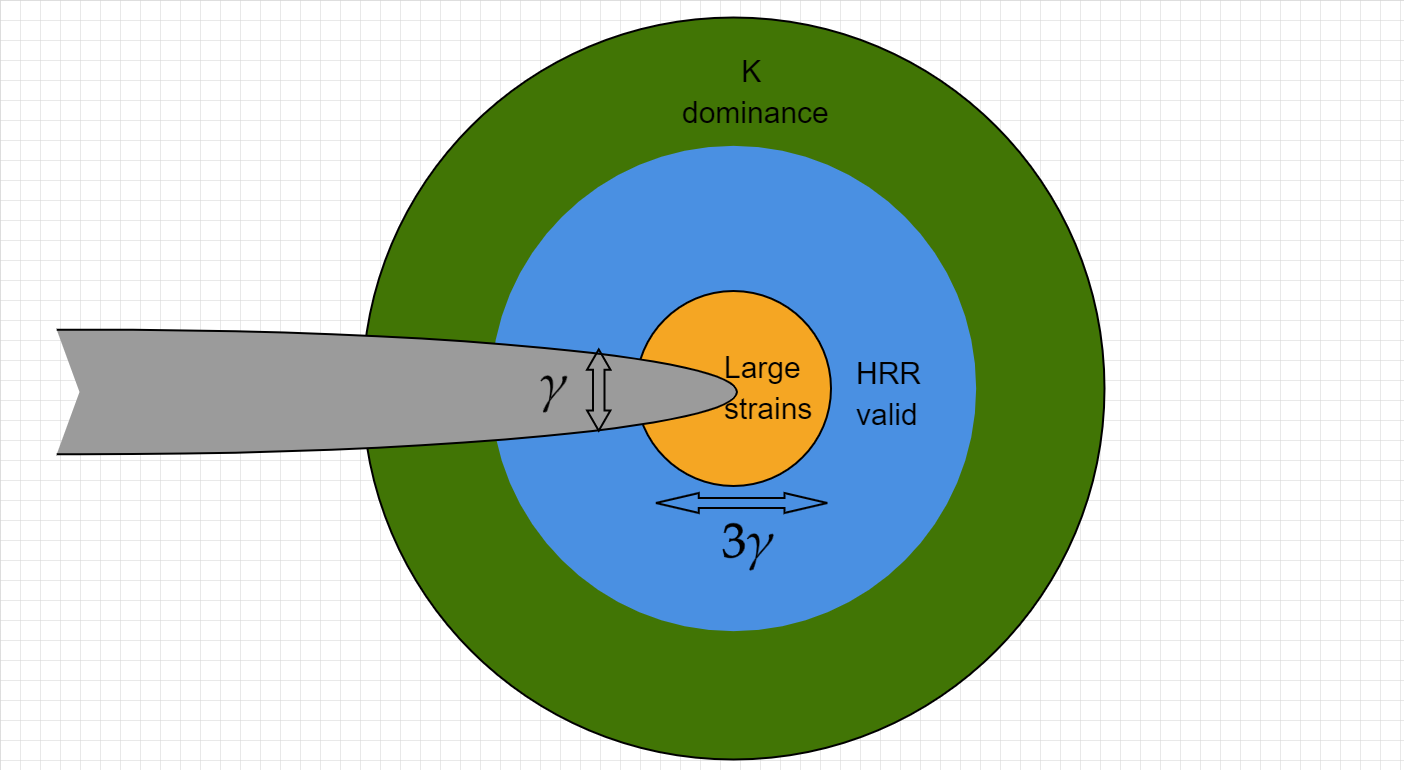
It is time to find the angular dependency of the stress and strain (but we wont)

To do so, one need to introduce a stress function \(\phi\) whose derivatives define \(\sigma\).

Crack growth resistance curves

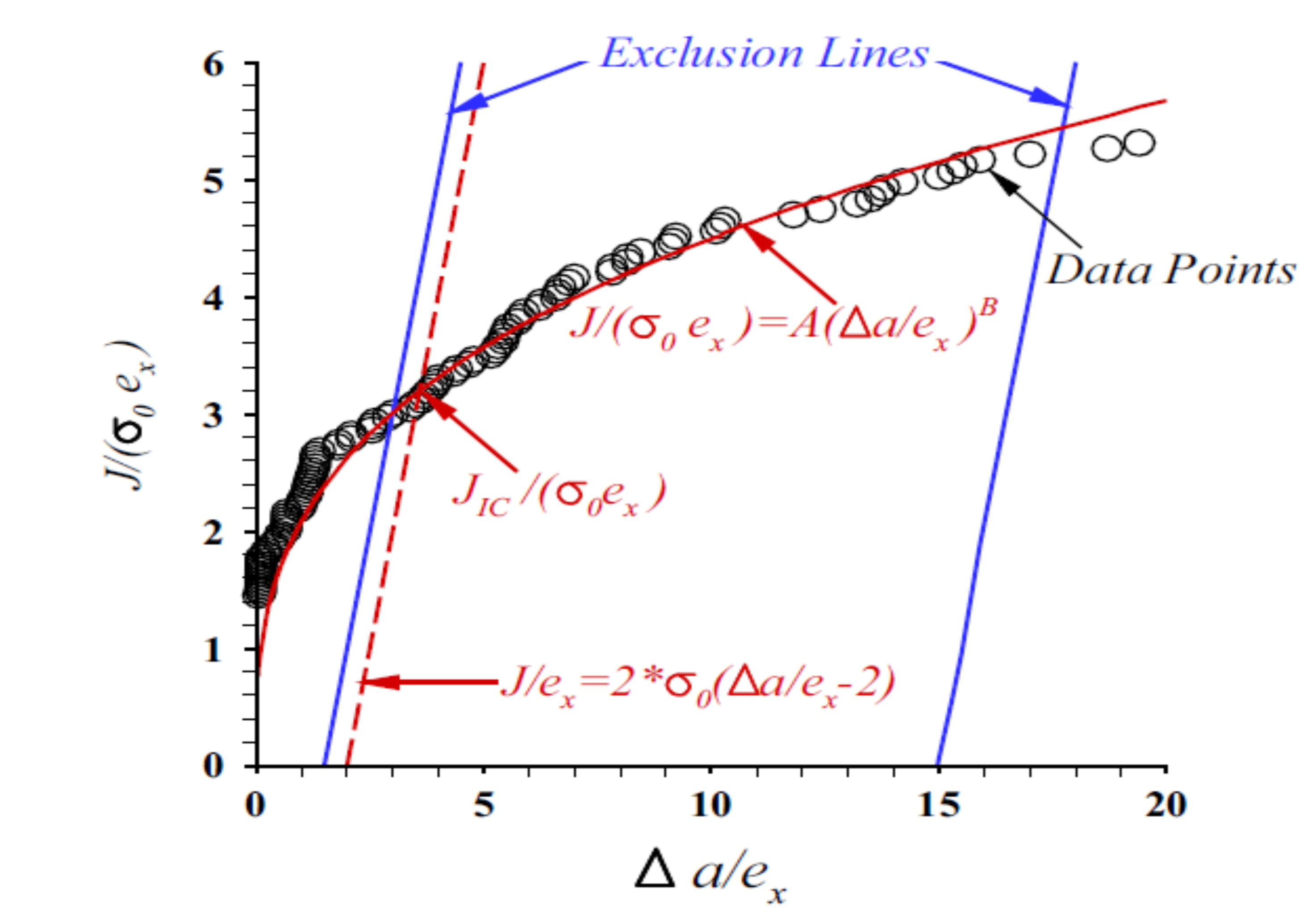
The value of the tearing modulus is calculated by applying:

\[ T_R = \frac{E}{\sigma_0^2}\frac{dJ}{da} \]

on the polynomial fit to the data points between the exclusion lines.

Similar to the way we handeled \(G\) we can examine the stability of a growing crack by comparing the driving force for crack growth as :

\[\begin{split} T_{app}=\frac{E}{\sigma_0^2}\left( \frac{dJ}{da}\right )_{\Delta_T} \\ \\ \ \ \\ \Delta T = \color{red}{\Delta} + \color{blue}{C_mP} \end{split}\]

with \(\color{red}{\Delta}\) being the applied displacement and \(\color{blue}{C_m,P}\) being the machine compliance and applied load.

We can easily obtain

\[ \left( \frac{dJ}{da}\right )_{\Delta_T} = \left( \frac{dJ}{da}\right )_{P}-\left( \frac{dJ}{dP}\right )_{a}\left( \frac{d\Delta}{da}\right )_{P} \left [ C_m+\left(\frac{\partial \Delta}{\partial P }\right)_a \right]^-1 \]

When the machine is infinitely stiff (\(\color{blue}{C_m} \to \infty\) - load control) we are left with

\[ \color{blue}{\left( \frac{dJ}{da}\right )_{\Delta_T} = \left( \frac{dJ}{da}\right )_{P}} \]

A crack will grow in a stable manner when \(J=J_R\) and \(T_{app} \leq T_R\)

A crack will grow in an unstable manner when \(J=J_R\) and \(T_{app} \gt T_R\)