Fracture on the Atomic Scale

We have seen that Inglis’s solution yield:

\[ \sigma_{max} = \sigma_{\inf} \left( 1+\frac{2a}{b} \right) = \sigma_{\inf} \left( 1+ 2\sqrt{\frac{a}{\rho} }\right) \]

In the limit where \(a>>b\) we obtain that \(\rho \to 0\) and thus:

\[ \sigma_{max} = 2\sigma_{\inf} \left( \sqrt{\frac{a}{\rho}} \right ) \]

So lets ask our self what is the smallest \(\rho\) that has a physical meaning?

The Lennard-Jones potential is one of the early models for describing the potential energy between two atoms. In its general form it is formulated as the sum of a \(\color{red}{\text{repulsive}}\) and \(\color{blue}{\text{attractive}}\) terms and attains a minimum at \(r_{eq}=2^{1/m}\sigma\) :

\[ U(r) = k\epsilon \left[ \color{red}{\left ( \frac{\sigma}{r} \right ) ^n} - \color{blue}{\left( \frac{\sigma}{r} \right) ^m} \right] \]

The figure below shows the LJ potential with \(\sigma = 2.4193\), \(\epsilon = 0.2007\) and \(m=6;n=12\) resulting in \(r= 2.7156\)

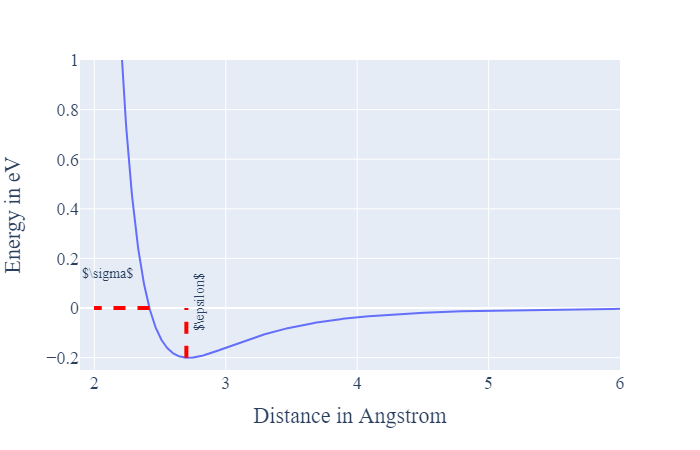
The forces acting on the atoms can be calculated by taking the derivative of \(U\)

For a crack to form, we need to separate two atomic layers. In other words, we need to apply a tensile force which will be sufficiently high to overcome the cohesive force and extend the interatomic distance from \(r_{eq}\) to a sufficiently large distance such that \(U(r)=0\).

For simplicity, let us assume that the cohesive strength can be taken as:

\[ F = F_0 \sin\left( \frac{\pi r}{\lambda}\right) \]

With \(\Lambda\) being the distance required to completely separate the two atomic layers. For small displacements, \(\sin x \approx x\) and we can write:

\[ F=\color{green}{F_0 \left( \frac{\pi}{\lambda}\right)} r \]

The \(\color{green}{\text{prefactor}}\) of \(r\) is an approximation of the Young’s modulus (think of a spring) and \(F_0\) is the maximum force needed to overcome the attractive forces between the atoms. multiplying everything by the length of the atomic layer (number of bonds to be broken) we can rewrite the equation to read:

\[ \sigma_{cohesive} = \frac{E \lambda}{\pi r_0} \]

and assuming that \(\lambda/x_0 \approx 1\) we obtain

\[ \sigma_{cohesive} \approx \frac{E}{\pi r_0} \]

We can estimate the energy required to perform this separation process by integrating the force over the separation distance :

\[ \gamma_{s} = \frac{1}{2} \int_{0}^{\lambda}{\sigma_{cohesive}\sin \frac{\pi x}{\lambda} dx} = \frac{\sigma_{cohesive} \lambda}{\pi} \]

Finally, from the last two equations we obtain :

\[ \sigma_{cohesive} = \sqrt{\frac{E \gamma_s}{x_0}} \]

Going back to Inglis’s solution we can assume that the smallest radius is of the order of one interatomic distance \(x_0\) and then that

\[ \sigma_{max} = 2\sigma_{\inf}\sqrt{\frac{a}{x_0}} \]

and by equating \(\sigma_{max}\) and \(\sigma_{cohesive}\) we obtain:

\[ \sigma_{fracture} = \sqrt{\frac{E \gamma_s}{4a}} \]