Griffith’s Energy Balance

We will now follow Griffith and try to analyze the external stresses required to fracture a plate with an elliptical crack.

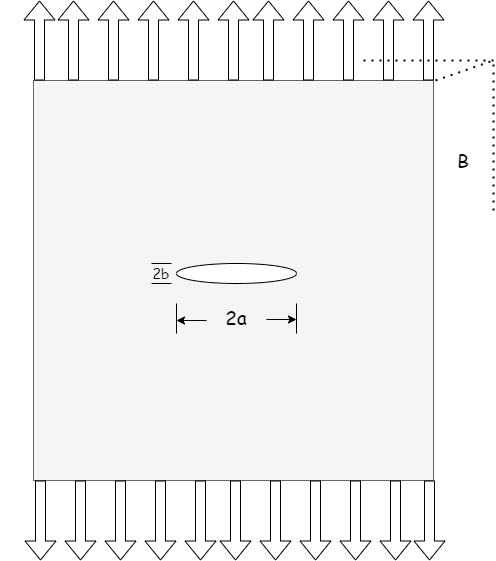
We can write the potential energy on the plate as :

\[ U = U_0 - {\color{red} U_{crack}} + {\color{blue} U_{surface}} \]

Where \(U_0\) is the elastic energy in the uncracked plate and utilizing Inglis’s solution for an elliptical crack :

\[\begin{split} \begin{align*} &\color{red} {U_{crack}} = \frac{\pi a^2 \sigma_{\inf} ^2 B}{E} \\ \\ \quad \\ &\color{blue} {U_{surface}} = 2 \left( 2aB\gamma_s\right) \end{align*} \end{split}\]

Crack growth will take place only if \(\frac{dU}{d a}\) will indicate that an increase in \(a\) is energetically favorable. Looking at \(\frac{d U}{d a}=0\) we can thus identify the critical crack length for a given magnitude of remote loading:

\[\begin{split} \begin{align*} \color{red}{ \frac{dU_{crack}}{da}} = \color{blue}{ \frac{dU_{surface}}{da}} \\ \\ \quad \\ \color{red} {\frac{\pi a \sigma_{\inf}^2}{E}} = \color{blue} {2\gamma_s} \\ \\ \quad \\ a_{eq} = \frac{2\gamma_s}{\pi}\frac{E}{\sigma_{\inf}^2} \end{align*} \end{split}\]

rearranging and isolating \(\sigma_{\inf}\) we arrive at

\[ \sigma_{fracture} = \left( \frac{2E\gamma_s}{\pi a}\right)^{1/2} \]

Note that the Griffith fracture criteria is completely ignorant of the radius at the ellipse tip.

Some small modofications

A revised expression of Griffith’s criteria can be written by replacing the surface energy \(\gamma_s\) with a more general term - \(w_f\) the fracture energy.

\(w_f\) can be used to account for the presence of plasticity:

\[ w_f = \gamma_s + \gamma_p \]

Or to account for crack tortuosity : $\( w_f = \gamma_s * \left ( \frac{A_{true}}{A_{projected}} \right) \)$