Airy’s Stress Functions

Airy’s stress functions pose a useful technique for solving two dimensional linear elasticity problems in equilibrium.

Given a two dimensional continuous and isotropic elastic body, subjected to external tractions \(t_i(x_1,x_2)\)

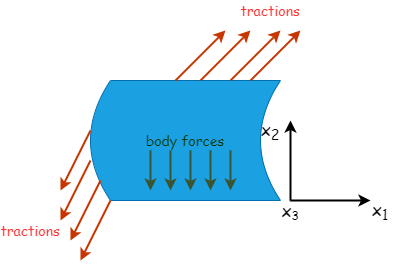
and assuming that the body forces can be written as a derivative of a scalar function of positions such that :

\[ \rho F_1 = \frac{\partial \Omega}{\partial x_1} \quad ; \quad \rho F_2 = \frac{\partial \Omega}{\partial x_2} \quad ; \quad \rho F_3 = 0 \text{ (!2D)} \]

there exist a function \(\Phi(x_1,x_2)\) for which :

\[ \nabla^2\nabla^2\Phi = \frac{\partial^4{\Phi}}{\partial x^4} +2\frac{\partial^4{\Phi}}{\partial x^2 \partial y^2} +\frac{\partial^4{\Phi}}{\partial y^4} =\left ( \frac{\partial F_1}{\partial x_1} + \frac{\partial F_2}{\partial x_2}\right)C(\nu) \]

where

\[\begin{split} C(\nu) = \begin{cases} \frac{1}{1-\nu},& \text{plane stress}\\ \\ \frac{1-\nu}{1-2\nu},& \text{plane strain} \end{cases} \end{split}\]

For the case on no body forces \(\Phi\) satisfied the bi-harmonic equation

\[ \nabla^2\nabla^2\Phi = \frac{\partial^4{\Phi}}{\partial x^4} +2\frac{\partial^4{\Phi}}{\partial x^2 \partial y^2} +\frac{\partial^4{\Phi}}{\partial y^4} =0 \]

After demanding that \(\Phi\) satisfies the boundary conditions, we can use \(\Phi\) to derive the stresses:

\[ \sigma_{xx} = \frac{\partial^2{\Phi}}{\partial{y}^2} \quad ; \quad \sigma_{yy} = \frac{\partial^2{\Phi}}{\partial{x}^2} \quad ; \quad \tau_{xy} = \frac{\partial^2{\Phi}}{\partial{x}\partial{y}} \]

\(\Phi\) is guaranteed to satisfy both \(\color{red}{\text{equilibrium}}\) and \(\color{green}{\text{compatability}}\) equations automatically:

\[\begin{split} \begin{align*} & \color{red}{\frac{\partial \sigma_{xx}}{\partial x} +\frac{\partial \tau_{xy}}{\partial y} =0} \quad ; \quad \color{red}{\frac{\partial \sigma_{yy}}{\partial y} +\frac{\partial \tau_{xy}}{\partial x} =0 } \\ \\ & \color{green}{\nabla^2\left ( \sigma_{xx} + \sigma_{yy}\right ) = 0 } \end{align*} \end{split}\]

We can use the the constitutive relation to extract the strains from the stresses and if the displacement filed is sought after, the strains can be integrated.

Airy stress functions in polar coordinates

In polar coordinates, where \(u_{\theta}\) and \(u_r\) represent the tangential and radial displacements, the strains are given by:

\[ \epsilon_{rr} = \frac{\partial u_r}{\partial_r} \quad ; \quad \epsilon_{\theta \theta} = \frac{1}{r}\frac{\partial u_{\theta}}{\partial_{\theta}} + \frac{u_r}{r} \quad ; \quad \epsilon_{r \theta} = \frac{1}{2} \left ( \frac{1}{r}\frac{\partial u_{r}}{\partial_{\theta}} +\frac{\partial u_{\theta}}{\partial_{r}} - \frac{u_{\theta}}{r} \right) \]

and the \(\color{red}{\text{equilibrium}}\) and \(\color{green}{\text{compatability}}\) equations are:

\[\begin{split} \begin{align*} &\color{red}{\frac{\partial \sigma_{rr}}{\partial r} +\frac{1}{r}\frac{\partial \tau_{r \theta}}{\partial \theta} + \frac{\sigma_{rr} - \sigma_{\theta \theta}}{r} =0} \quad ; \quad \color{red}{\frac{1}{r}\frac{\partial \sigma_{\theta \theta}}{\partial \theta} +\frac{\partial \tau_{r \theta}}{\partial r} + \frac{2\tau_{r \theta}}{r} =0} \\ \\ &\color{green}{\nabla^2\left ( \sigma_{r r} + \sigma_{\theta \theta} \right ) = 0 } \end{align*} \end{split}\]

In polar coordinates, stresses are expressed as:

\[\begin{split} \begin {align*} \sigma_{rr}& = \frac{1}{r^2} \frac{\partial^2 \Phi}{\partial \theta ^2} + \frac{1}{r}\frac{\partial \Phi}{\partial r}\\ \\ \tau_{r \theta}& = \frac{1}{r^2} \frac{\partial^2 \Phi}{\partial \theta \partial r} + \frac{1}{r^2}\frac{\partial \Phi}{\partial \theta} \\ \\ \sigma_{\theta \theta}& = \frac{\partial ^2 \Phi}{\partial r^2} \end{align*} \end{split}\]

Next, we will see how to obtain the stress field around a circular hole in an infinite plate subjected to arbitrary remote tractions using Airy’s stress function.