Kirsch’s Infinite Plate
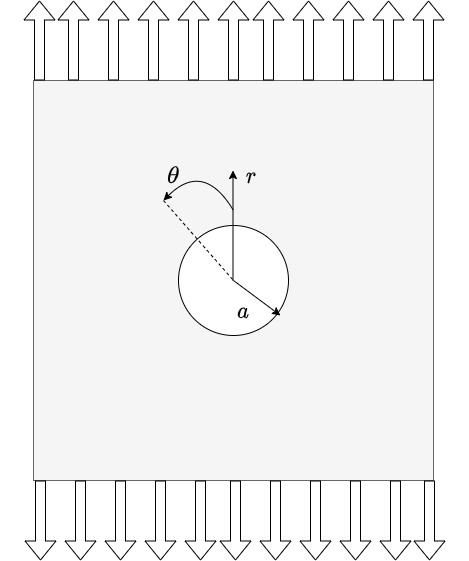
Consider a 2D plate containing a circular hole and being subjected to remote tensile load \(\sigma_{\inf}\).
Taking under consideration the boundary conditions, we require our stress to be zero on the hole’s free surface:
\[
\sigma_r (r=a, \theta) = \tau_{r \theta} (r=a, \theta)=0
\]
We will start by considering a circular portion of the plate concentric with the hole and having a radius large enough with resect to a. The stresses will effectively be the same as in the plate without the hole and thus:
\[\begin{split}
\begin{align*}
& \sigma_r =\sigma_{\inf} cos^2 \theta = \sigma_{\inf} \frac{1}{2} (1+cos2\theta) \\
\\
& \tau_{r \theta} = -\sigma_{\inf} \frac{sin 2\theta}{2} \\
\end{align*}
\end{split}\]
The stress distribution in the plate can be regarded as having two parts, the first arising from the normal applied traction and is \(\frac{\sigma_{\inf}}{2}\) and the second part having an angular dependence.
A good guess for \(\Phi\), seems to have the general form :
\[ \Phi = g(r) + f(r)cos2\theta \]
Let us ignore \(g(r)\) for now.
Substituting \(\Phi\) into the bi-harmonic equation we readily obtain:
\[
\left ( \frac{d^2}{dr^2} + \frac{1}{r}\frac{d}{dr} - \frac{4}{r^2} \right )\left ( \frac{d^2 f}{dr^2} + \frac{1}{r}\frac{df}{dr} - \frac{4f}{r^2} \right ) = 0
\]
A general solution to this ODE on \(f(r)\) will have the form :
\[ f(r) = Ar^2 + Br^4 + \frac{C}{r^2} + D \]
and so the stress components are
\[\begin{split}
\begin {align*}
& \sigma_{rr} = \frac{1}{r^2} \frac{\partial^2 \Phi}{\partial \theta ^2} + \frac{1}{r}\frac{\partial \Phi}{\partial r} = -\left( 2A +\frac{6C}{r^4} + \frac{4D}{r^2}\right)cos 2 \theta\\
\\ \\
& \tau_{r \theta} = \frac{1}{r^2} \frac{\partial^2 \Phi}{\partial \theta \partial r} + \frac{1}{r^2}\frac{\partial \Phi}{\partial \theta} = \left( 2A + 6Br^2 - \frac{6C}{r^4} - \frac{2D}{r^2}\right)sin 2 \theta \\
\\
& \sigma_{\theta \theta} = \frac{\partial ^2 \Phi}{\partial r^2} = \left( 2A + 12Br^2 + \frac{6C}{r^4}\right)cos 2 \theta
\end{align*}
\end{split}\]
From the conditions prescribed above we obtain:
\[
A= - \frac{1}{4} \sigma_{\inf} \quad ; \quad B=0 \quad ; \quad C=-\frac{a^4}{4}\sigma_{\inf} \quad ; \quad D=\frac{a^2}{2}\sigma_{\inf}
\]
The uniform tension \(\frac{1}{2}\sigma_{\inf}\) is accounted for by \(g(r)\) which can be written as :
\[
g(r) = A_1log (r) + B_1r^2log(r) +C_1r^2 + D_1
\]
which is a general solution for a stress distribution symmetrical about an axis.
Adding the two parts of the solution we finally obtain:
\[\begin{split}
\begin{align*}
\sigma_{rr} &= \frac{\sigma_{\inf}}{2} \left( 1 - \frac{a^2}{r^2}\right) + \frac{\sigma_{\inf}}{2} \left( 1 + \frac{3a^4}{r^4} - \frac{4a^2}{r^2}\right)cos2\theta \\
\\
\sigma_{r\theta} &= -\frac{\sigma_{\inf}}{2} \left( 1 - \frac{3a^4}{r^4} + \frac{2a^2}{r^2}\right) sin2\theta\\
\\
\sigma_{\theta \theta} &= \frac{\sigma_{\inf}}{2} \left( 1 + \frac{a^2}{r^2}\right) - \frac{\sigma_{\inf}}{2} \left( 1 + \frac{3a^4}{r^4}\right)cos2\theta \\
\end{align*}
\end{split}\]
For \(r=a\) we can see that
$\(
\sigma_{rr}=\tau_{r \theta} =0 \quad ; \quad \sigma_{\theta \theta} = \sigma_{\inf} \left(1-2cos2\theta \right)
\)$
the maximum stress experienced appear at \(\theta = \pi /2 ; 3\pi/2\) where \(\sigma_{\theta \theta} = 3\sigma_{inf}\)
Note that for \(\theta=0,\pi\) we obtain \(\sigma_{\theta \theta}=-\sigma_{\inf}\).
From the figure below, it is evident that the stress magnitude rapidly decreases to the remote load as \(r\) increases.



