Mixed Mode Fracture

Motivation

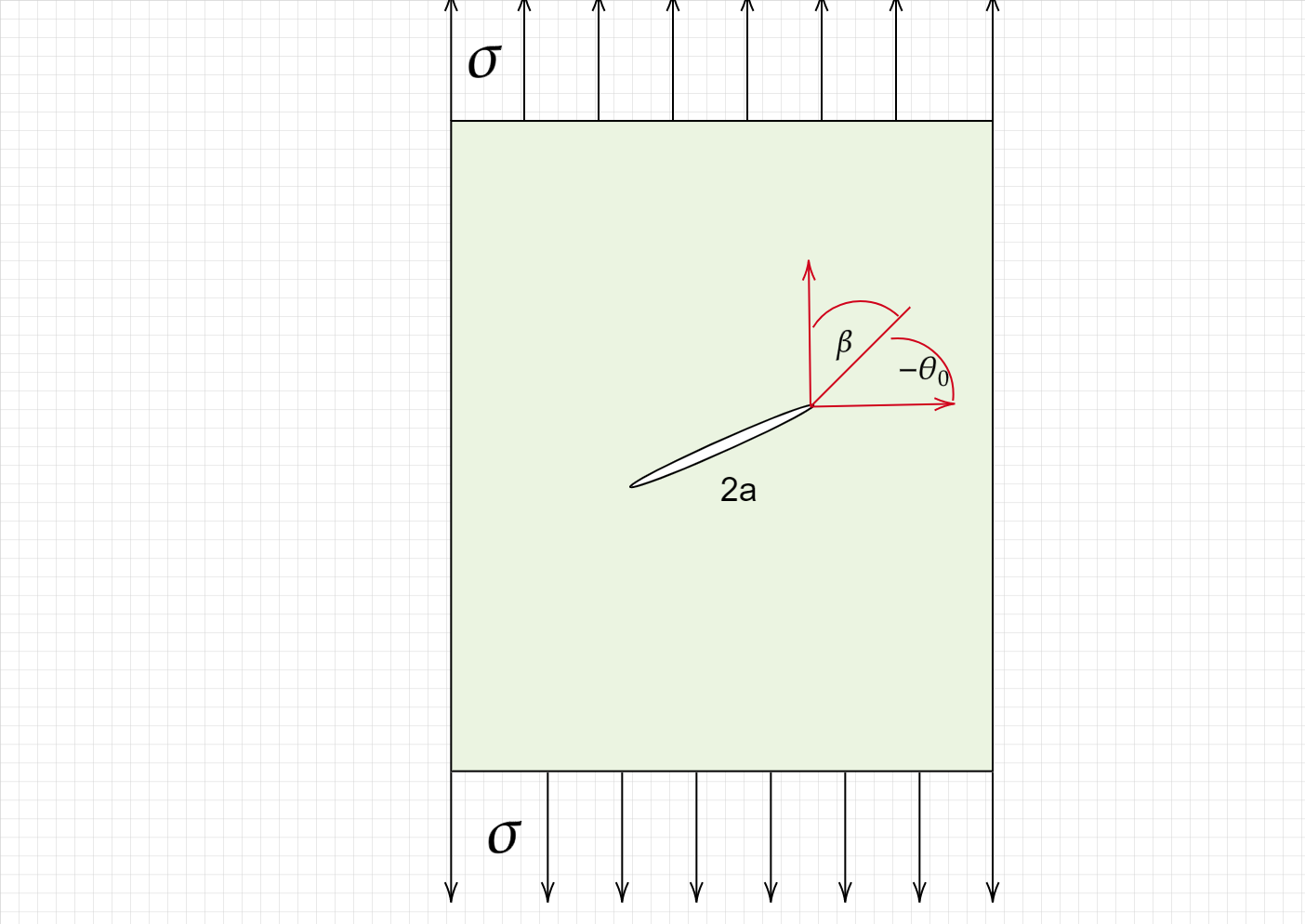
So far we have discussed mostly mode I cracks (tensile) however real life scenarios will often involve not only tensile tractions ths leading to mixed mode interactions

Mixed-mode scenarios will often be found in heterogenous structures (multi-phase materials, weldements, coatings, composites etc.).

We can use superposition and obtain the crack tip fields as

\[\begin{split} \sigma_{11} = \frac{K_I}{\sqrt{ 2 \pi r}} \left [ \cos \frac{\theta}{2} \left ( 1- \sin \frac{\theta}{2} \sin \frac{2\theta}{2} \right ) \right ] +\frac{K_{II}}{\sqrt{ 2 \pi r}} \left [ -\sin \frac{\theta}{2} \left ( 2+ \cos \frac{\theta}{2} \cos \frac{2\theta}{2} \right ) \right ] \\ \sigma_{22} = \frac{K_I}{\sqrt{ 2 \pi r}} \left [ \cos \frac{\theta}{2} \left ( 1+ \sin \frac{\theta}{2} \sin \frac{2\theta}{2} \right ) \right ] +\frac{K_{II}}{\sqrt{ 2 \pi r}} \left [ \sin \frac{\theta}{2} \cos \frac{\theta}{2} \cos \frac{2\theta}{2} \right ] \\ \sigma_{12} = \frac{K_I}{\sqrt{ 2 \pi r}} \left [ \cos \frac{\theta}{2} \sin \frac{\theta}{2} \sin \frac{2\theta}{2} \right ] +\frac{K_{II}}{\sqrt{ 2 \pi r}} \left [ \cos \frac{\theta}{2} \left ( 1- \sin \frac{\theta}{2} \sin \frac{2\theta}{2} \right ) \right ] \end{split}\]

And the displacements:

\[\begin{split} u_1 = \frac{K_I}{2 \mu} \sqrt{ \frac{r}{2 \pi}} \left [ \cos \frac{\theta}{2} \left ( \kappa - \cos \theta \right ) \right ] +\frac{K_{II}}{2 \mu} \sqrt{ \frac{r}{2 \pi}} \left [ \sin \frac{\theta}{2} \left ( \kappa - + \cos \theta \right ) \right ] \\ u_2 = \frac{K_I}{2 \mu} \sqrt{ \frac{r}{2 \pi}} \left [ \sin \frac{\theta}{2} \left ( \kappa - \cos \theta \right ) \right ] +\frac{K_{II}}{2 \mu} \sqrt{ \frac{r}{2 \pi}} \left [ - \cos \frac{\theta}{2} \left ( \kappa -2 + \cos \theta \right ) \right ] \end{split}\]

Energy release rate

We can write the total energy release write to be

\[\begin{split} G = \frac{K_I^2}{E'}+\frac{K_{II}^2}{E'} + \frac{(1+\nu)K_{III}^2}{E} \\ E' = E/(1-\nu^2) \ \ \text{for plane strain} \\ E' = E \ \ \text{for plane stress} \end{split}\]

Assuming we already measured the critical value of \(G_I=G_{IC}=\frac{K_{IC}^2}{E'}\)

We can see that for mixed mode loading we obtain

\[ K_{IC}^2=K_I^2+K_{II}^2+\frac{E'(1+\nu)}{E}K_{III}^2 \]

Question

What is the meaning of the expression we just obtained?

For the 2D problem sketched above we can write the stresses as

\[\begin{split} \sigma_{xx} = \sigma \cos^2\beta \\ \sigma_{yy} = \sigma \sin^2\beta \\ \tau_{xy} = \sigma \cos\beta\sin\beta \\ \end{split}\]

leading to

\[\begin{split} K_I = \sigma_{yy}\sqrt{\pi a} = \sigma \sqrt{\pi a} \sin^2 \beta\\ K_{II} = \tau_{xy}\sqrt{\pi a} = \sigma \sqrt{\pi a} \sin \beta\cos\beta \end{split}\]

and then

\[ K_{IC}^2 = K_I^2 + K_{II}^2 \rightarrow K_{IC}=\sigma_f \sqrt{\pi a} \sin \beta \]

Example

Consider a plate with a \(10mm\) crack at angle \(\beta\) subjected to an applied stress of \(130 MPa\). Assuming that the \(K_{IC}\) is known and equal \(25 MPa\sqrt{m}\) find out if the plate will fail for any value of \(\beta\)

Using the above equations we can find the values of \(K_I\) and \(K_{II}\) as a function of the angle to be

\[\begin{split} K_I = 130MPa\sqrt{\pi 10e-3}\sin^2\beta = 23\sin^2\beta MPa\sqrt{m}\\ K_{II} = 130MPa\sqrt{\pi 10e-3}\sin\beta\cos\beta =\sin\beta\cos\beta MPa\sqrt{m}\\ \end{split}\]

and then

\[ \sqrt{K_I^2+K_{II}^2} = 23*\sqrt{\sin^4\beta + (\sin\beta\cos\beta)^2} \]

This expression will always yield a result smaller than \(25MPa\sqrt{m}\)

Under mixed mode conditions, cracks may propagate at an inclined angle (\(\theta_c\)) to their original direction (\(\beta\))

Writing \(\theta_c=\frac{\pi}{2}-\beta\) and using the \(K_{IC}\) expression we obtain

\[ K_{IC} = \sigma_f \sqrt{\pi a} \cos\theta_C \]

I the crack will grow aligned with the \(x\) direction, this will lead to \(K=K_I\) and \(K_{II} \to 0\).

For some materials, it was observed that the relation

\[ \K_{IC} = \sqrt{\frac{2}{3}} \]

is a better approximation to the mixed-mode conditions leading to

\[ K_I^2 + \frac{2}{3}K_{II}^2 = K_{IC}^2 \]

Which leads to

\[ K_{IC} = \sigma_f \sqrt{\frac{\pi a}{3} (3-\cos^2\beta)}\sin\beta \]

Principle stress

The principle stress criterion requires that the crack will grow in the direction perpendicular to the maximum principal stress.

\[\begin{split} \frac{\partial \sigma_{\theta \theta}}{\partial \theta} = 0 \ \ \text{for} \theta=\theta_c \\ \frac{\partial^2 \sigma_{\theta \theta}}{\partial \theta^2} < 0 \ \ for \sigma_{\theta \theta}>0 \end{split}\]

Considering the same 2D problem as before, and setting \(\tau_{r \theta}=0\) (so that \(\sigma_{\theta \theta}\) will become a principal stress) we can rewrite the expressions for the stress intensity factors :

\[\begin{split} K_I \sin \theta_c + K_{II}(3\cos\theta_c -1)=0 \\ \end{split}\]

we define \(K_r = \frac{K_I}{K_{II}}\) to obtain

\[ \theta_c = -\arccos \frac{1}{3}\left [ 1 - \frac{K_r (K_r -3 \sqrt{K_r^2+8} }{K_R^2+9}\right ] \ \ \text{for} \ \ \theta_c<\frac{pi}{2} \]

This gives us a way of finding the crack growth direction if we know \(K_r\)

For a pure mode II loading we will obtain \(\theta_c = -70.53^o\)

The maximum principle stress can be derived to be (some trgo which we skip) :

\[ \sigma_{\theta}(\theta=\theta_c) = \frac{1}{\sqrt{2\pi r}}\cos\frac{\theta_c}{2}^2 \left [ K_I\cos\frac{\theta_c}{2} - 3K_{II} \sin \frac{\theta_c}{2} \right] \]

and using the definition of \(K_{IC}\) for a pure mode I we obtain

\[ K_{IC} = K_I\cos^3\frac{\theta_c}{2} - 3K_{II} \sin \frac{\theta_c}{2} \cos^2 \frac{\theta_c}{2} \]

Looking at the angle for a pure mode II (\(\theta_c = -70.53\)) we can see that under this criterion

\[ K_{IIC} = 1.15K_{IC} \]

Strain energy density criterion

Sih proposed that the strain energy density \(S\) dictates the crack growth direction such that crack growth will start in the direction for which :

\[\begin{split} \frac{\partial S}{\partial \theta} = 0 \\ \frac{\partial^2 S}{\partial \theta^2} > 0 \\ \end{split}\]

To use this criterion we thus have to define \(W_c\) at \(\theta=\theta_c\).

The strain energy can be derived using the stress fields and the definition of work done on a body to obtain

\[\begin{split}S = &K_I^2 \frac{1}{16G} [ (1+\cos \theta)(\kappa -\cos \theta)] \\ + &K_{II}^2 \frac{1}{16G} [(\kappa +1) (1-\cos \theta) + (1+\cos \theta)(3\cos \theta -1)] \\ + &K_I K_{II} \frac{1}{16G}\sin \theta [ 2\cos \theta) -(\kappa -1)]\end{split}\]

Excersice

Consider the same plate as before being subjected to a mixed mode loading under plane strain conditions. We are given with the following inputs:

• The plate fractures if \(\sigma_{yy} = 150MPa\) or \(\tau_{xy}=90MPa\)

• The crack length is \(a=30 mm\)

• \(\nu = 0.33\) and \(E=\195GPa\)

Use the strain energy density criteria to calculate:

1. \(\theta_c\)

2. \(\beta\)

3. \(K_IC\) and \(K_{IIC}\)

Compare the results to what you would have obtained using the maximum principle stress criterion.

Guidance principla stress

1. Find the stress intensity factors.

2. Find \(K_r\)

3. Use the equation we derived for \(\theta_c\) based on \(K_r\)

4. FInd \(\beta\)

5. Calculate \(K_{IC}\) and \(K_{IIC}\)

strain energy density

1. calculate \(\kappa\)

2. use the relation between \(S\) and the stress intensity factors to find \(\theta_c\) by taking the derivative with respect to \(\theta\) as \(0\) and setting \(\theta= \theta_c\) 3.Calculate \(K_{IC}\) and \(K_{IIC}\)

3. Find \(S_C\)