CTOD - Crack Tip Opening Displacement

In the early 60’s, A. Wells was measuring the mode I fracture toughness (\(K_{IC}\)) of structural steels when he noticed that the toughness they exhibit is too high to be characterized by linear elastic fracture mechanics.

Wells than proposed a failure criterion based on the observation that in the presence of crack-tip plasticity, the crack tip appears to blunt with the application of load before a crack emerges.

Moreover Wells noted that the blunting process appeared to increase proportionally to the tested materials toughness.

Using Irwin’s crack-tip plasticity model, Wells was able to show that the CTOD (\(\delta\)) follows:

\[ \delta = \frac{4}{\pi}\frac{G}{\sigma_y} \]

A similar result is obtained following the strip model:

\[ \delta = \frac{G}{m \sigma_y} \]

and \(m\) assumes a value of \(1\) for plane stress and \(2\) for plane strain.

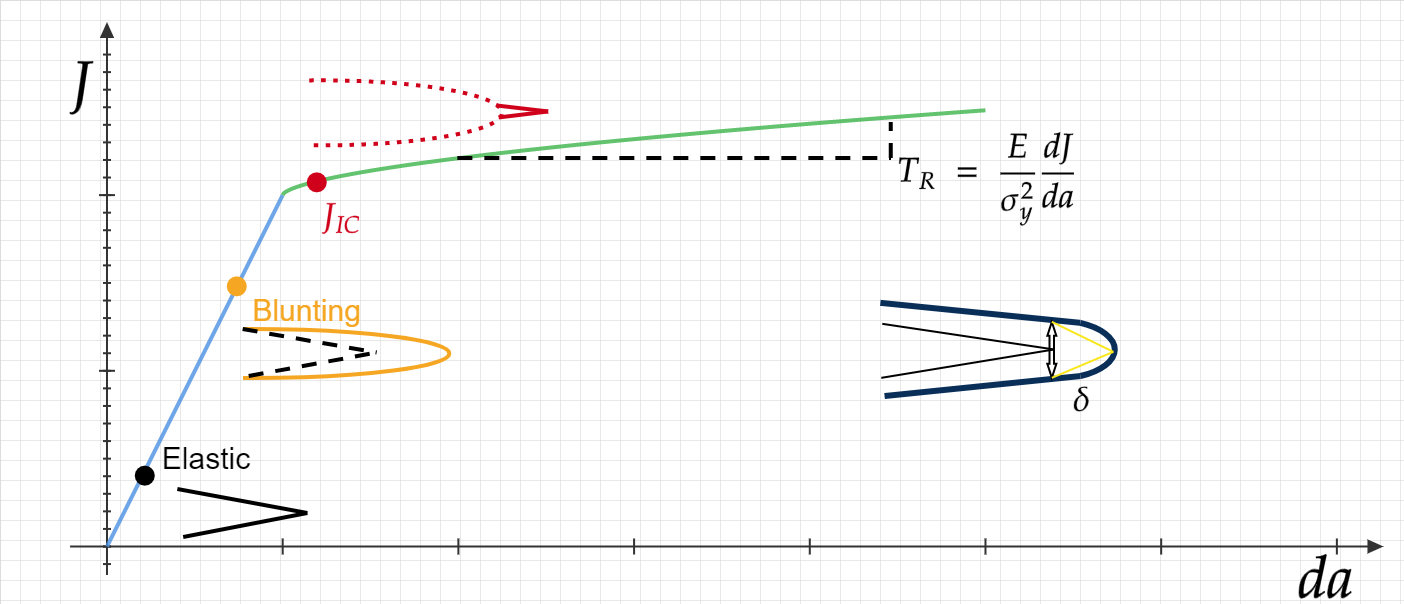
The CTOD is defined in one of the two ways shown above. However the two expressions are only identical for a semicircle blunting crack.

During the process of crack tip blunting, the crack faces ae gradually moving apart, and using the assumption of rigidity they can be assumed to rotate around a hinge point.

While not entirely accurate, this assumption allows us to measure the Crack Mouth Opening Displacement (CMOD) and using similarity of triangles obtain the CTOD.

\[ \delta_{CTOD} = \frac{r(W-a)}{r(W-a)+a} \delta_{CMOD} \]

The experimentaly measured CMOD is decomposed into an elastic and plastic part (similar to the way you would for a stress strain curve) and thus:

\[ \delta_{CTOD} = \delta_{e} + \delta_{p} = \frac{K_I^2}{m\sigma_y E'} + \frac{r(W-a)}{r(W-a)+a} \delta_{CMOD} \]

J-CTOD

From the above relation it is easy to see that when LEFM holds we obtain

\[ J=m\sigma_y \delta_{CTOD} \]

Using the strip model for crack tip plasticity it is simple to demonstrate that for a non-hardening elasto-plastic material undergoing crack tip blunting:

\[ J=\sigma_y \delta_{CTOD} \]

In 1981, Shih demonstrated using the HRR solution that :

\[ \delta_{CTOD} = d_n \frac{J}{\sigma_y} \]

Where \(d_n\) is a dimensionless constant which depends on the strain hardening exponent \(n\) and on \(\alpha \frac{\sigma_y}{E}\).