Inglis Solution¶

In 1913, Inglis proposed a solution for the stress field surrounding an elliptical hole in an infinite plate subjected to remote loading1. The ellipse equation is given by :

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} =1 \]

and the smallest radius of the ellipse at the major a-axis is given by \(\rho = \frac{b^2}{a}\)

While Inglis’s solution may be viewed as a generalization of Kirsch’s solution, it is in fact of much greater relevance for our purposes. As we will see, taking the extreme case of an ellipse as a sharp crack will bring us one step closer to understanding the effects of crack on the strength of materials.

Inglis’s solution, is based on generalizing the 2D polar coordinates we previously used. This “new” set of coordinates is known as elliptical coordinates (in fact this is a subset of a wider family of coordinates known as curvilinear coordinates which we will use again when discussing slip lines theory).

They are defined using two sets of curves \(\alpha\) and \(\beta\) which will intersect with one another at a right angle.

\[\begin{split} x=c\cosh \alpha \cos \beta \\ \\ \quad \\ y=c\sinh \alpha \sin \beta \\ \end{split}\]

For remote loading in the direction perpendicular to the major axis of the ellipse, Inglis’s solution yields the following stresses at y=0:

\[\begin{split} \begin{align*} &\sigma_x =\sigma_{inf} \left [ \frac{-1}{\color{red}{A^2}} + \frac{x(x^2-a^2+b^2)^{-1/2}}{\color{red}{A^2}} - \frac{a^2x(x^2-a^2+b^2)^{-3/2}}{\color{red}{A}}\right] \\ \\ \quad \\ &\sigma_y = \sigma_{\inf} \left[ 1-{\color{blue}{B}} + {\color{blue}{B}} x (x^2-a^2+b^2) ^{-1/2} - \frac{a^2x(x^2-a^2+b^2)^{-3/2}}{\color{red}{A}} \right] \end{align*} \end{split}\]

With

\[ {\color{red}{A} = 1-\frac{b}{a}} \quad ; \quad {\color{blue}{B} = \frac{1-\frac{2b}{a}}{(1-\frac{b}{a})^2}} \]

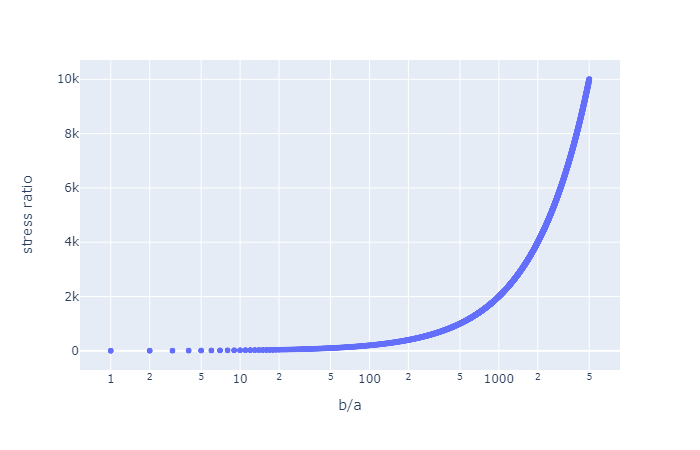
The maximum stress is then given by:

\[ \sigma_{max} = \sigma_{\inf}\left(1+\frac{2a}{b} \right) \]

for \(a=\) the ellipse vecomes a circle and Kirsch’s solution is recovered. However, as \(b \to 0\) a singularity is approached and \(\sigma_{max} \to \infty\).

1: C.E. Inglis, “Stresses in a Plate Due to the Presence of Cracks and Sharp Corners,” Transactions of the Institution of Naval Architects, Vol. 55, London, 1913, pp. 219–230

FM036004-Notes

Inglis Solution¶