Crack tip elements#
Typically, “regular” elements, placed at the crack tip lead to poor convergence and are replaced by “special” elements know as crack-tip elements.
The key behind CTE is to utilize shape functions which are capable of describing the analytical crack tip fields, and more specifically the \(1/\sqrt{r}\) singularity. The \(\theta\) dependence can be satisfacory described by the elements arrangment.
Quarter point (Barsoum) elements#
QP elements are based on translating nodes from the mid-side of the element to a quarter length distance from the crack tip.
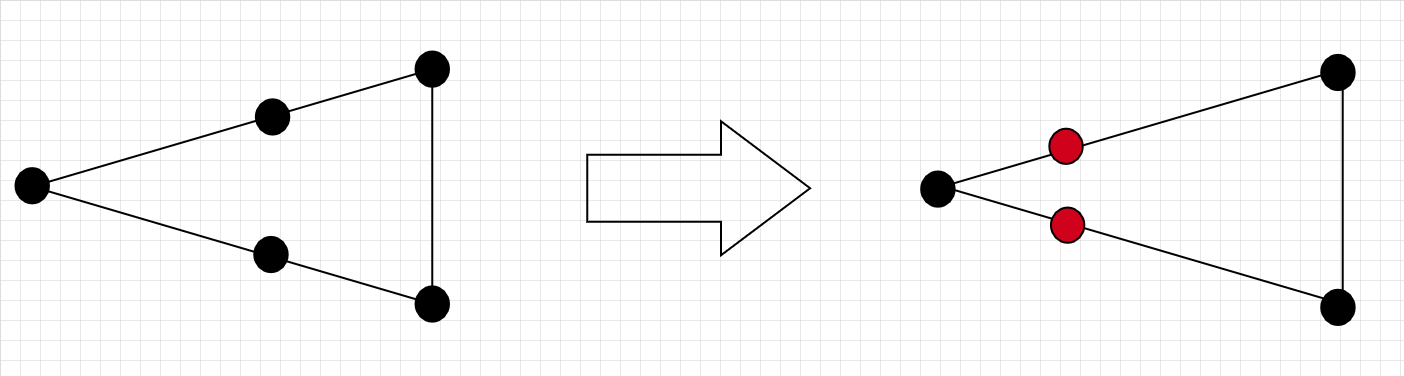
The mapping of the isoparametric coordinates to the local coordinates lead to a singular term compatibale with the analytical stress fields.
Consider a 1D element for which the displacement field is given by :
\[
u(\xi) = \sum _{a=1}^3 N_a(\xi)u^{(a)}
\]
