9. Stress Waves in Solids¶

The Wave equation

\[ \frac{\partial^2 u}{\partial t^2} = {\color{blue}{C}}^2\sum_i \frac{\partial^2 u}{\partial x_i^2} \]

Consider a “1D” (i.e. \(L>>\phi\)) rod whose end is extended following \(V(t)=\dot{u}\)

Since the body can not be said to be in rest the sum of forces on the body is given by

\[ \sum F = ma =m\dot{V} = m\ddot{u} \]

Looking at an infinitesimal element within our rod we can construct the free body diagram:

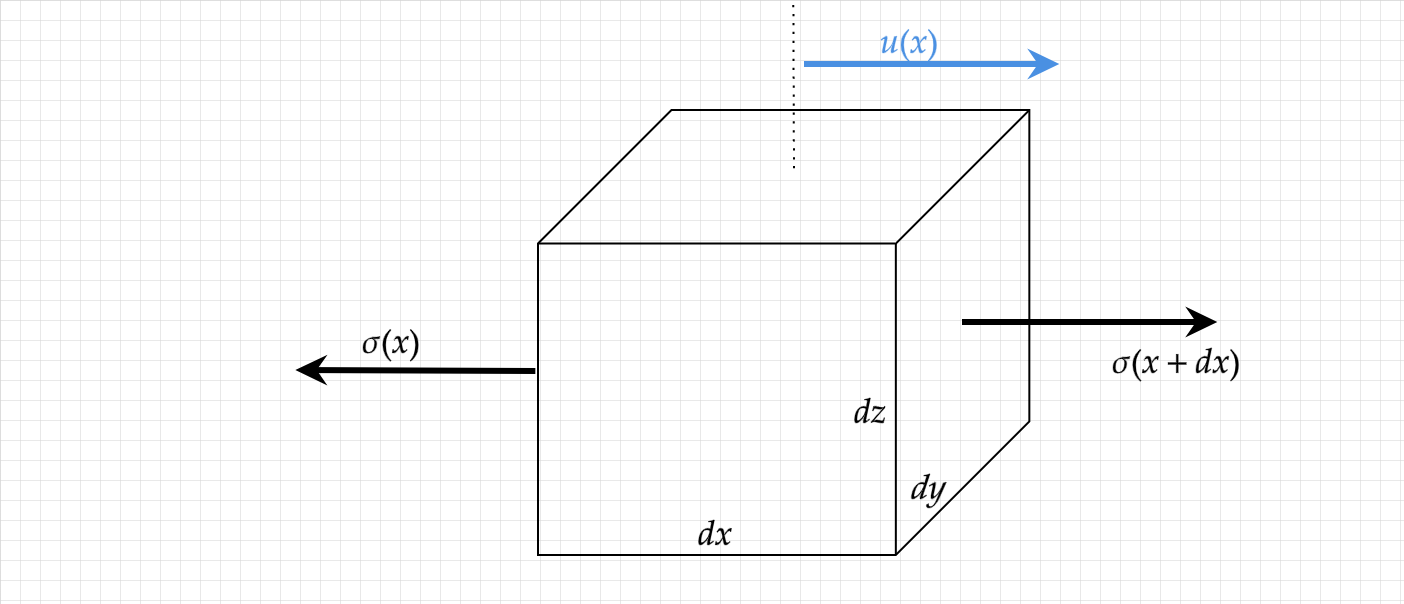
from which we can see that

\[ \left [ \sigma(x+dx) -\sigma(x) \right ]dyxz = \rho dx dy dz \ddot{u} \]

taking \(dx \to 0\) we obtain:

\[ \frac{\partial \sigma}{\partial x} = \rho \ddot{u} \]

Assuming linear elasticity , and recalling that \(\epsilon=\frac{\partial u}{\partial x}\) the above equation can be written as

\[ {\color{blue}E}\frac{\partial^2 u}{\partial x^2} = {\color{blue}\rho} \frac{\partial^2 u}{\partial t^2} \]

or

\[ \frac{\partial^2 u}{\partial t^2} = {\color{blue}{C_L}}^2 \frac{\partial^2 u}{\partial x^2} \ \, \ \ \text{with} \ \ {\color{blue}{C_L=\sqrt{\frac{E}{\rho}}}} \]

Note

Under shear stresses a similar expression can be derived leading to \({\color{red}{C_S=\sqrt{\frac{G}{\rho}}}}\)
For those of you interested in stress waves ME036006 is highly recommended.
Here and here you can find more information as well as some animations of different waves.

Question

When we conduct a simple tensile test, waves are constantly running through the system. Still we treat this as a Quasi-static problem. Why?

We can define a (scale dependent) characteristic time by considering

\[ \Delta t = \frac{L}{\color{blue}{C_L}} \]

For the same bar, we can write the natural frequencies of longitudinal vibration as:

\[ f_n = \frac{n{\color{blue}{C_L}}}{2L} \]

ME034044notes

Stress Waves in Solids

9. Stress Waves in Solids¶