.md .pdf

Contents

12. Temperature Measurments

Temperature measurement has a key role in process monitoring.

For many industrial processes a precise and acurate temperature measurment (with timely response) can be the deciding factor between success and failure. Moreover, in many cases the cost of the process can be reduced by properly monitoring the temperature.

Among the various applications where temperature measurments can be found are:

1. Metal production and processing.

2. Petro-chemical industry.

3. Climate control.

4. Quantum computers.

5. Medical devices (e.g. MRI)

When considering the desired characteristics of a Temperature sensor we must also consider the application it self (as always).

In addition we should think of other questions such as:

1. To what extent is my sensor affected by factors other than the temperature (e.g. humidity, pressure)

2. Where will the sensor be positioned (should we use a contact or non-contact sensor)

3. Should we provide special protection to the sensor?

12.1. Contact Thermometers

12.1.1. Thermocouples

Principal of operation

A thermocouple is based on the Seebeck effect - A cunducting material will generate a voltage when experiencing a thermal gradient.

A thermocouple consists of a a couple of metals attached at two nodes and as such they will produce a voltage (electromotive force) proportional to the temperature difference \(\Delta T\) between them such that

\[ V_s = S\Delta T \]

The conversion between the measured voltage and temperature is dependent on the two metals used for constructing the thermocouple.

For each thermocouple, we need to know the Seebeck cooeficient which is usually given as a polynom such that:

\[ V_s =\sum_{i=0}^n c_i (t_{90})^i \]

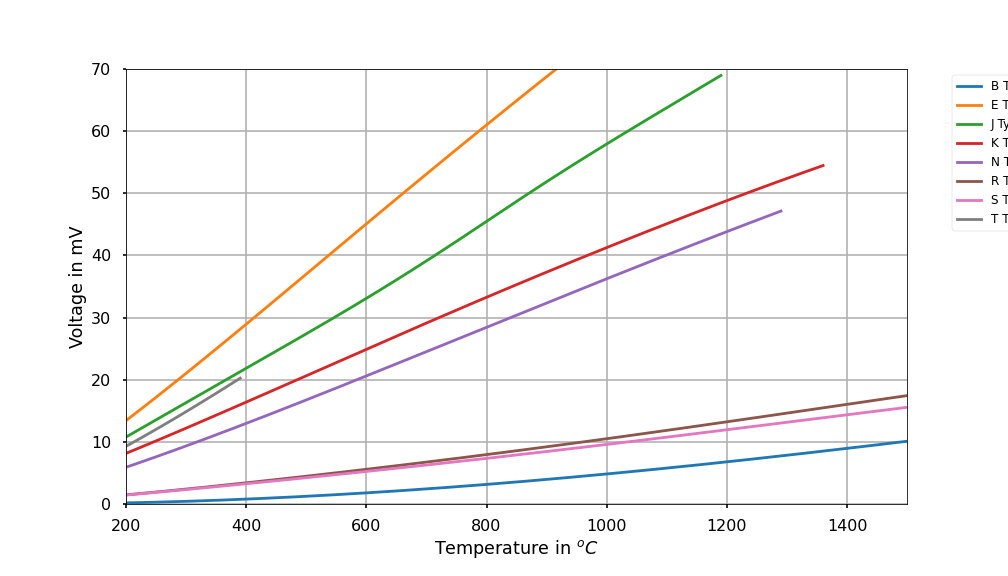
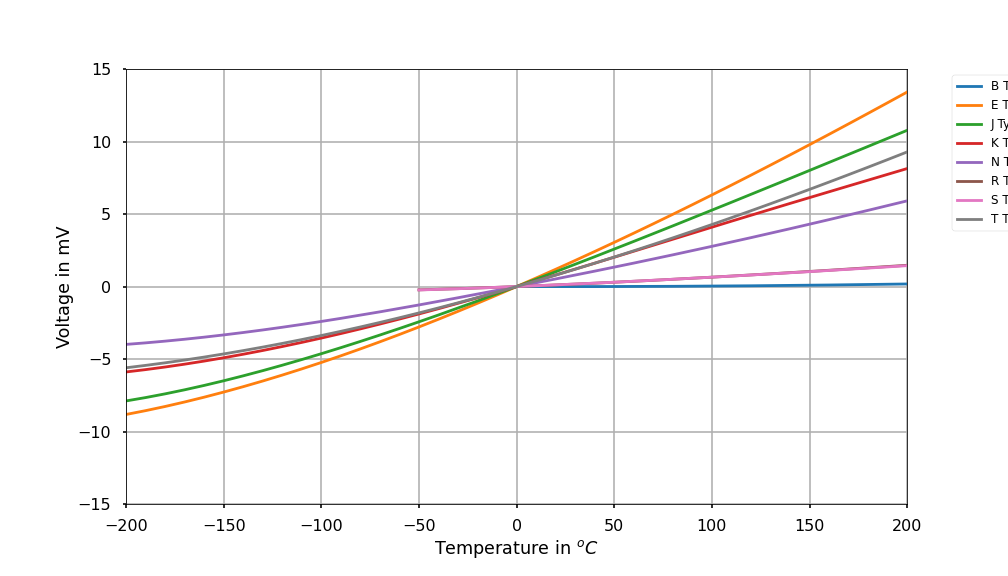
For K type thermocouples there is an extra term :

\[\begin{split} V_s =\sum_{i=0}^n c_i (t_{90})^i + a_0 e^{a_1 (t_{90}-a_2)^2}\\ a_0 = 0.118597600000\times10^0 \\ a_1 = - 0.118343200000\times10^{-3} \\ a_2 = 0.126968600000 \times 10^3 \end{split}\]

Type	Composition	Temp. Range [\(^oC\)]
\(K\)	Ni-Cr alloy vs. Ni-Al alloy	\(-270 \to 1372\)
\(T\)	Cu vs. a Cu-Ni alloy	\(-270 \to 400\)
\(B\)	Pt-30% Rh vs. Pt-6% Rh	\(0 \to 1820 \)
\(E\)	Ni-Cr alloy vs. a Cu-Ni alloy	\(-270 \to 1000 \)
\(J\)	Fe versus a Cu-Ni alloy	\(-210 \to 1200\)
\(N\)	Ni-Cr-Si alloy vs. Ni-Si-Mg alloy	\(-270 \to 1300\)
\(R\)	Pt-13% Rh vs. Pt	\(-50 \to 1768\)
\(S\)	Cu vs. a Cu-Ni alloy	\(-50 \to 1768\)

The coefficients \(c_i\) for each type can be found in NIST Thermocouples coefficients data

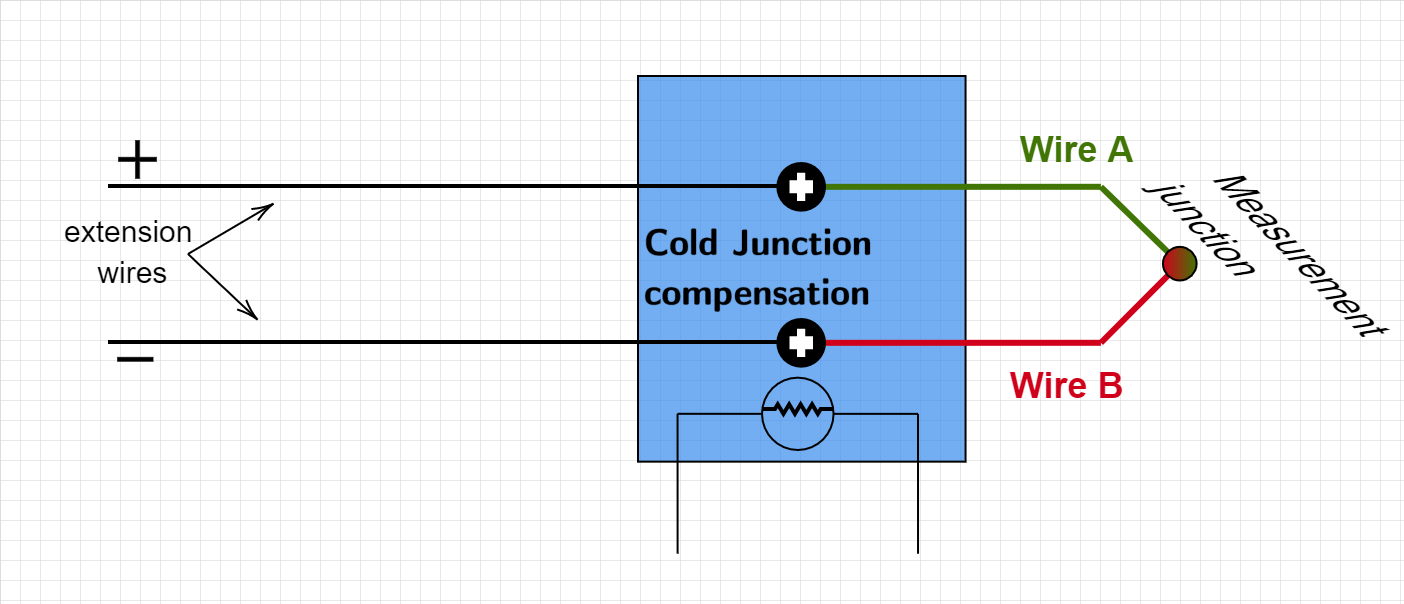
Since the resulting Voltage is not a mere function of the Temperature itself but rather of the gradient, we must know the temperature at the reference junction ( where the voltage measurement is made).

The tables in the NIST database are for a reference temperature \(T_{ref}=0^oC\), which can be achived by submerging the reference junction in ice water.

As you can imaginge, for many applications this is simply out of the question. An alternative, is to use what is commonly known as a”Cold junction compensation”.

12.1.2. Thermistor

Principal of operation

Thermistors are made of different semiconductive oxides. Most thermistors exhibit a strong (negative) dependence of resistance on temperature.

The resistance of NTC type thermistor follow the Steinhart-Hart relation :

\[\begin{split} R_T = R_0 \exp \left [ B\left ( \frac{1}{T} - \frac{1}{T_0} \right)\right ] \\ \text{} \\ \ \ \text{Or} \\ \text{} \\ \frac{1}{T} = \sum_{n=0}^{\infty}a_n \left ( ln\frac{R}{R_0}\right)^n \end{split}\]

Thermistors offer a good sensitivity albeit a small temperature range of operation and demonstrate a fast response time.

When using a thermistor a current will flow through it (we need to measure the resistance somehow…)

As a result, heat will generated (remember when we discussed S.G?) and will induce self heating.

To reduce this effect, thermistors with high resistance are used (typicaly of the order of Kilo-ohms)

Note

The response time of a thermistor is influenced by factors such as the dimensions and shape (mass, surface area/volume ratio), the enacpsulating material, the enclosure and the thermistor manufacturing process.

Dont forget to make sure that \(\tau\) was measured for a temperature range similar to the one you will be working in and for the same medium (gas vs. liwuid for example)

12.1.3. Platinum resistance thermometer

Principal of operation

Made of a metallic wire/film and rely on variations in resistance with temperature.

Standard Platinum based RTDs can exhibit uncertainties as low as \(\pm 0.001 ^oC\). Other types of RTD, which are more suitable for out of the lab usage, exhibit a sensitivity of \(0.4mV/^oC\) (e.g. Pt100 sensor) and accuracy of \(\pm 0.01^oC\) for a limited temperature range (roughly up to \(200^oC\)).

While loosing some accuracy, RTDs can be used for up to \(~850^oC\).

12.2. Non-Contact Thermometers

12.2.1. Infrared radiation thermometers

Principal of operation

Planck’s law - The radiation of a black body, in thermal equilibrium with the surrunding, at a temperature \(T\) will emit radiation whose spectral density is given by

\[ B_{\nu}(T) = \frac{2h\nu^3}{c^2}\frac{1}{exp(h \nu / K_B T)-1} \]

Wien’s law - A black body will emit radiation, peaking at a wavelength proportional to \(1/T\)

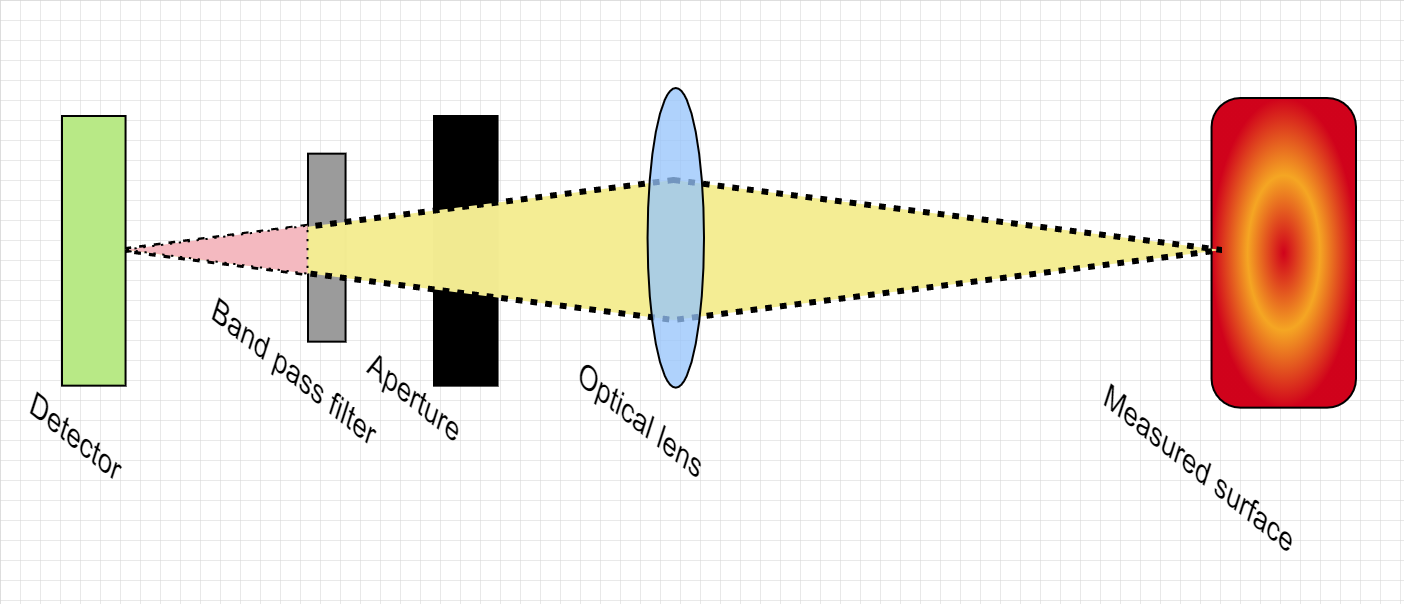
The detector is typically a photo-detector (photon\(\to\) electrical current). For many applications the detector are cooled down and this is especially important in relatively low temperature measurments as it help to reduce the SNR.

IR detectors usually operate at a rather limited range, chosen by the wavelength where the seperation of black body radiation curves is maximal.

HgCdTe photodiode - \(8-14 \mu m\)

InSb photodiode - \(3-5 \mu m\)

Si photodiode - \(0.65 - 1 \mu m\)

For real bodies, the radiation is lower than that of a black body, and the emmisivity of the body is required for correcting the measurement (0 - no radiation ; 1 perfect black body).

IR detectors exhibit a measurement resolution better than \(0.1^oC\) but rather low accuracy (Typically of the order of \(1^oC\))

previous

11. Strain Measurments

next

13. Force Measurments