Vibrations in Beams
10. Vibrations in Beams¶
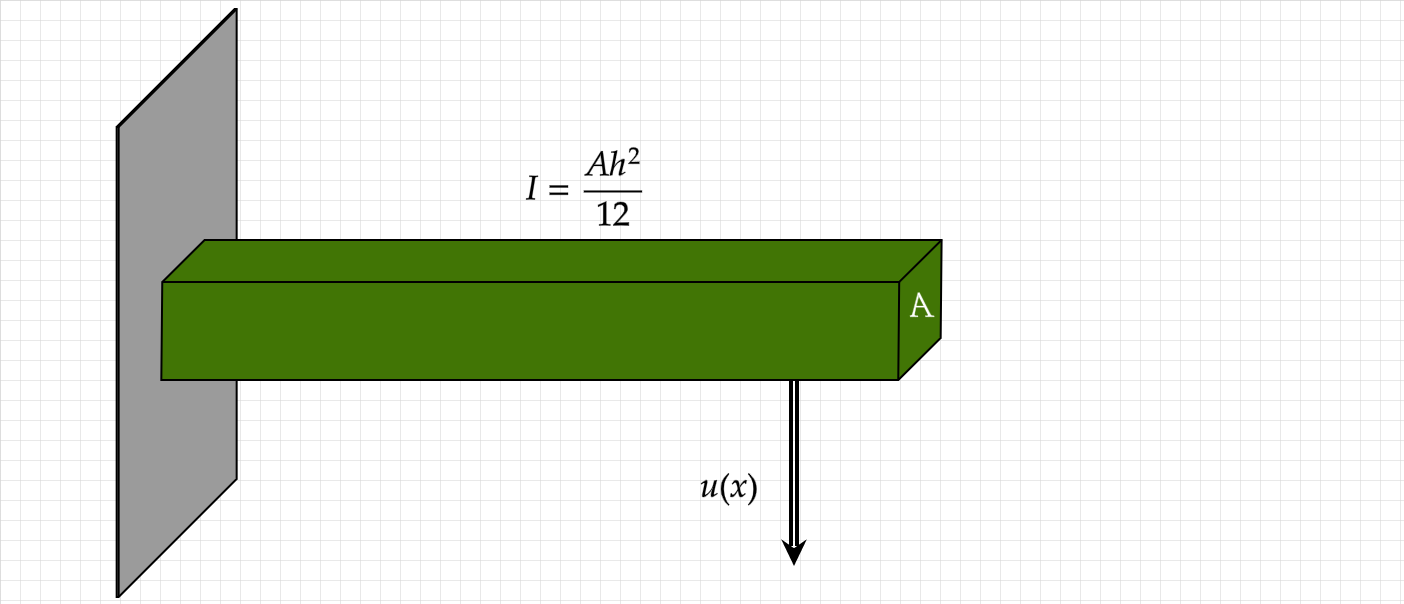
The Euler Bernoulli beam equation
\[
{\color{blue}{q}} - EI\frac{\partial ^4 u}{\partial x^4} =0
\]
For \({\color{blue}{q}}= -\rho A \ddot{u}\) we arrive at:
\[
\frac{\partial ^2 u}{\partial t^2} =-\frac{h^2}{12}{\color{blue}{C_L}}^2\frac{\partial ^4 u}{\partial x^4}
\]
here
\[
f_1 = 0.586\frac{{\color{blue}{C_L}}h}{2L^2}
\]
Fracture Mechanics Clip-On Gages
A sensor (e.g. a clip-on gauge) based on bending strain measurement with \(L=8mm\) and \(h=0.5mm\) has a natural frequency of \(f_1 = 7.325KHz\)
The bridge in the load frame used for the same measurement (\(L=1m,h=2.5cm\)) has a natural frequency of \(f_1 = 36.6Hz\)
